How Warren Buffett Rigged a Cube Recreation with Invoice Gates Specific Occasions

Warren Buffett as soon as challenged Invoice Gates to an uncommon recreation of cube. Buffett positioned 4 cube on the desk and defined the principles. They’d every decide a die, roll it a bunch of occasions, and whoever rolled a better quantity extra usually would win. These weren’t numbered like normal cube. The everyday one via six have been changed with different numbers that diversified from die to die. As a supposed courtesy, Buffett invited Gates to choose his die first. This aroused suspicion, compelling Gates to examine the cube for himself after which insist that Buffett select first. 

Usually, selecting first in video games confers a bonus, so why have been these moguls dueling for second decide? The reply lies in a peculiar property of Buffett’s cube. To understand it, let’s examine an instance of comparable cube which have the identical property as these utilized by Buffett however which are simpler to research. 

How usually will die A roll greater than die B? As a result of there are simply three distinct numbers on every die, one third of the time, die A will roll a 9, which wins no matter B’s roll. One third of the time, A will roll a 1, which loses no matter B’s roll. And the remaining third of the time, A will roll a 5, which wins on two thirds of B’s rolls (those that flip up 3 or 4). Aggregating these observations with the principles of likelihood, we get that A beats B (⅓ x 1) + (⅓ x 0) + (⅓ x ⅔) = 5/9, or about 56 p.c of the time. An identical calculation yields an similar win share for B over C. That’s, B additionally beats C about 56 p.c of the time. So if A normally beats B and B normally beats C, then certainly A ought to normally beat C, proper? Mistaken! C truly beats A about 56 p.c of the time as nicely. 

We name these delinquent cubes intransitive cube. Many relations encountered in life exhibit the alternative, transitive property: If Alicia is older than Bruno and Bruno is older than Cassandra, then Alicia is older than Cassandra. That’s a legitimate deduction as a result of the relation “is older than” obeys the transitive property. Intransitive cube shock our intuitions as a result of the relation “usually rolls greater than” is not transitive, despite the fact that it looks like it needs to be. Notice that to roll greater than die B on common, die A doesn’t must at all times roll greater. And critically, there may be overlap between circumstances during which A beats B and A loses to C. This interleaving of the numbers on the faces allows the intransitivity.

With any set of intransitive cube, whoever chooses first in Buffett’s recreation bears a drawback, as a result of the second participant can at all times decide the die that’s prone to defeat their opponent’s alternative. Many individuals first encounter intransitive video games via rock paper scissors. Its cyclic successful construction ensures that no alternative uniquely outranks another. Buffett’s cube recreation is akin to tricking your opponent into asserting what they intend to throw subsequent in rock paper scissors—a mistake that may value them the sport. 

Stanford statistician Bradley Efron invented intransitive cube over 50 years in the past. Every die in Efron’s set of 4 beats one other a powerful two thirds (about 67 p.c) of the time. Martin Gardner popularized Efron’s cube in his legendary “Mathematical Video games” column at Scientific American, however mathheads have devised many intelligent variants since then. We now know that any variety of cube (higher than two) can exhibit an intransitive cycle, that means, for instance, there exists a set of 26 cube during which die A normally beats die B, which normally beats C, which normally beats D, and so forth all over to die Z, which, regardless of residing on the finish of an extended chain of dominating cube, pulls an upset by biking again and normally beating A.

Intransitive cube needn’t include six sides. In truth, intransitive trios of cube with any variety of sides (higher than two) exist. Dutch puzzle maker Oskar van Deventer even invented a set of seven six-sided cube that permit for 3 gamers in Buffett’s recreation. In different phrases, if Buffett and Gates invited Dolly Parton to play cube with them, then Gates and Parton may every take their decide from the seven, and Buffett would nonetheless at all times have a die within the remaining 5 that normally beats each of their decisions. 

Simply if you assume you’ve wrapped your head across the peculiar habits of intransitive cube, the sensible development under will roll you proper again to dumbstruck awe. 

One can calculate that A beats B 7/12 (about 58 p.c) of the time; B beats C 7/12 of the time; and C beats A 25/36 (about 69 p.c) of the time. To this point, nothing we haven’t seen earlier than. These don’t beat one another with similar possibilities, however they’re nonetheless intransitive. Typically cube are available pairs. If you think about rolling cube, you most likely image two similar cube in your hand and summing the numbers that flip up on every. What occurs if we roll pairs of cube from the determine above? What’s the likelihood that two copies of die A roll a sum that beats two copies of die B? Is it the identical as earlier than for the reason that copies are similar, or does duplicating the cube amplify the benefit that A has over B? In a surprising twist, the impact reverses. The pair of A cube normally lose to the pair of B cube! What’s extra, the entire cycle reverses: a pair of B cube normally lose to a pair of C cube and a pair of C cube normally lose to a pair of A cube. Procuring a set of those cube is a dependable method to get banned from household recreation evening. 

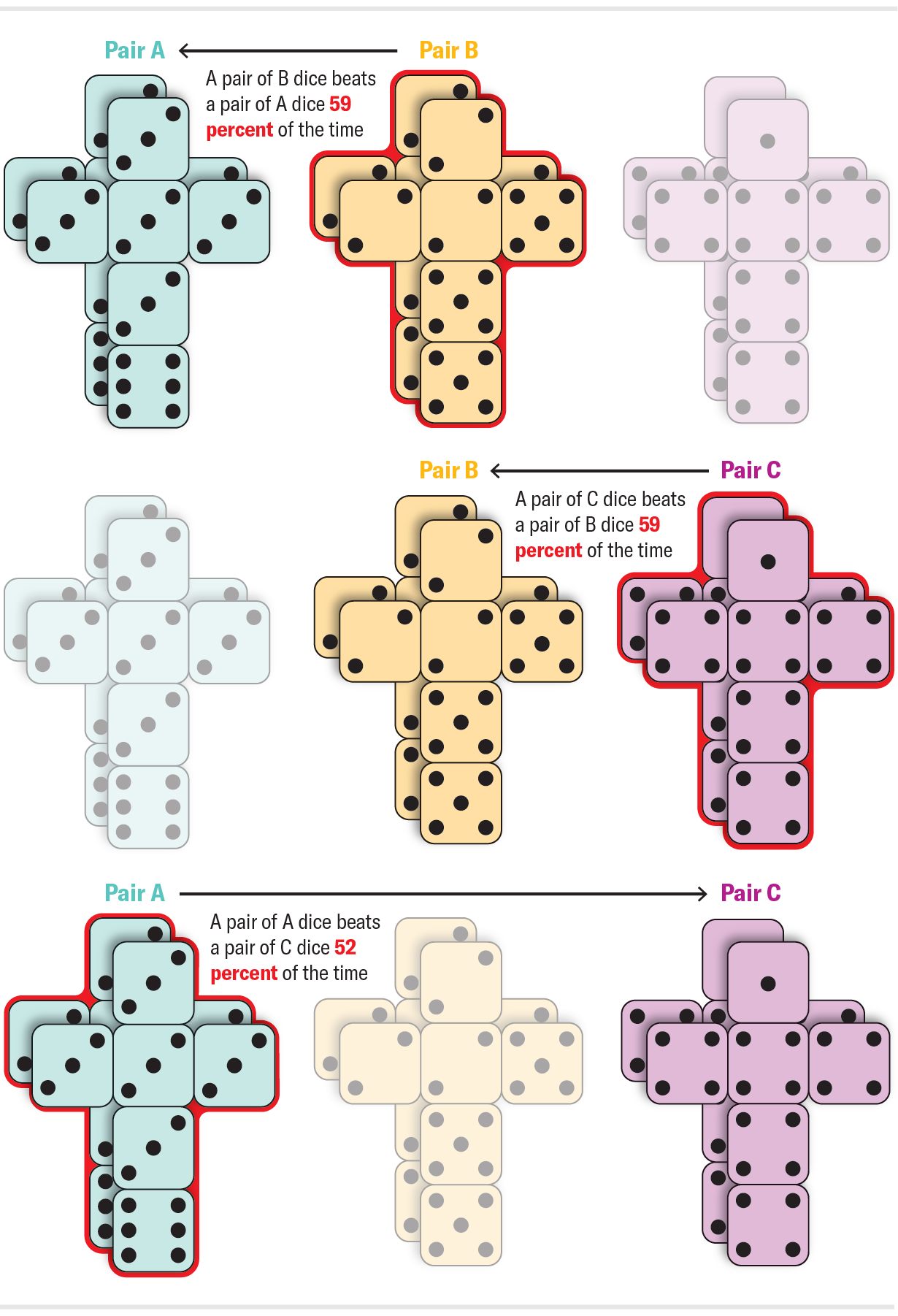
To get a really feel for the way duplicating cube may reverse their relative power, think about the easy case of two two-sided cube, X and Y. Each of X’s faces have a 1 on them, whereas Y’s faces are 0 and three. These cube have equal power. Y wins half of the time (when it rolls a 3) and loses half of the time (when it rolls a 0). After we duplicate the cube nonetheless, the Y pair turns into stronger than the X pair. The X pair at all times rolls a complete of two. The Y pair solely loses if each of them flip up 0, which solely occurs one quarter of the time. An identical phenomenon explains the reversal within the determine above.  

It’s not apparent that intransitive cube ought to exist in any respect. However is that as a result of they’re uncommon? If all a few trio of cube is that A normally beats B, and B normally beats C, is it extra possible that A normally beats C or vice versa? Intelligent folks have rigorously constructed by hand all the cube mentioned above, however may they’ve simply chosen cube numberings at random and had an honest shot at discovering an intransitive set? 

British mathematician Timothy Gowers got down to reply this query. Gowers leads the Polymath Undertaking, an modern and comparatively new paradigm for mathematical analysis. As an alternative of some mathematicians at one or two universities chipping away at an issue—the everyday analysis mannequin in math —the Polymath Undertaking takes a crowdsourcing method. Any variety of contributors can collaborate on a proof by way of on-line discussion board dialogue. Gowers deemed the intransitive cube query ripe for a gaggle effort and proposed it on his weblog in 2017. Changing a chalkboard with a WordPress feedback part, dozens of minds swarmed the issue and cracked it. 

Should you randomly assign numbers to a few completely different cube after which wish to know the probabilities that they exhibit intransitivity, it might rely upon what precisely you imply by “randomly assign numbers” to the cube. The polymath group modeled this with two pure standards. Simply as a typical six-sided die solely accommodates digits between 1 and 6, a random n-sided die will solely include digits between 1 and n (although some could repeat, and a few could not happen in any respect). Additionally, the numbers on a typical six-sided die add as much as 1 + 2 + 3 + 4 + 5 + 6. To maintain the cube balanced (e.g., no die ought to include all ones or solely huge digits), the polymath group required this of n-sided cube: the sum of their sides ought to equal the sum of the numbers from 1 to n.

Do you wish to guess whether or not transitive or intransitive cube are extra widespread? Polymath Undertaking individuals proved that three random n-sided cube might be intransitive about half of the time. In different phrases, realizing that A normally beats B, and B normally beats C, offers you virtually no details about whether or not A will normally beat C or vice versa. I’d have guessed that transitive cube have been extra widespread than intransitive ones. I may think about some suspicious readers, bored with having their expectations subverted, predicting that intransitive cube are extra widespread than transitive ones. However these slippery cube insist on evading prediction. For 3 cube, transitive and intransitive cube are equally widespread.

That is an opinion and evaluation article, and the views expressed by the creator or authors should not essentially these of Scientific American.